ToyGPT: A Miniature GPT Model for Arithmetic Addition

ToyGPT for Integer addition

Implemented a Transformer-based GPT model (Decoder-Only) for 2-digit integer addition using PyTorch. The project explores various architectural components of Transformers through a simple arithmetic task. The model takes concatenated input numbers as a string and predicts their sum in reverse order. Key aspects of the implementation include:

1. Positional Encoding Variants:

Compared Rotary Positional Encoding (RoPE), learnable Absolute Positional Encoding (APE), and No Positional Encoding (NoPE) to analyze their impact on model performance.

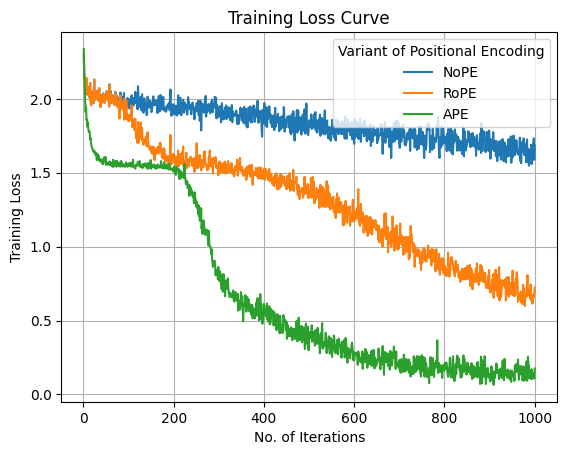
We observe that both the final training and test accuracy follow the order APE > RoPE > NoPE. This is intuitive, as the positional information of each digit is crucial for capturing the output of addition, and a learnable encoding performs better than a fixed positional encoding; however, the number of parameters for the learnable APE encoding is higher than the other two due to the learnable parameters.

2. Layer Normalization Exploration:

Investigated Pre-Layer Normalization, Post-Layer Normalization, and No-Layer Normalization configurations to assess their effects on training stability and accuracy.

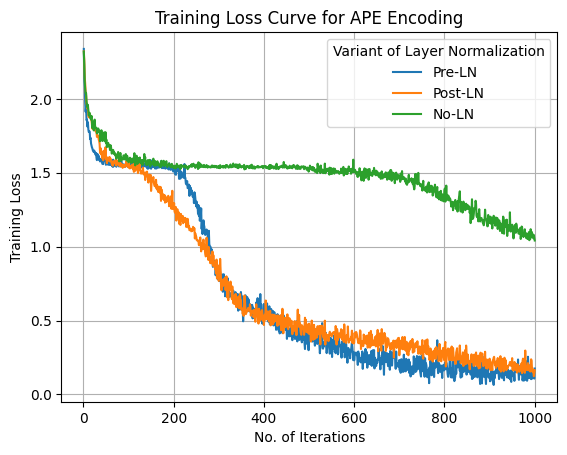
The final training loss for both Pre-LN and Post-LN is very similar, with Pre-LN performing better overall, including in final training and test accuracies. In contrast, without layer normalization, the training loss decreases slowly over iterations, and the final training loss is significantly higher, leading to lower final training and test accuracies.

3. Attention Map Visualization:

Implemented visualization of attention matrices for each head and layer, enabling analysis of attention patterns and their role in the addition task.

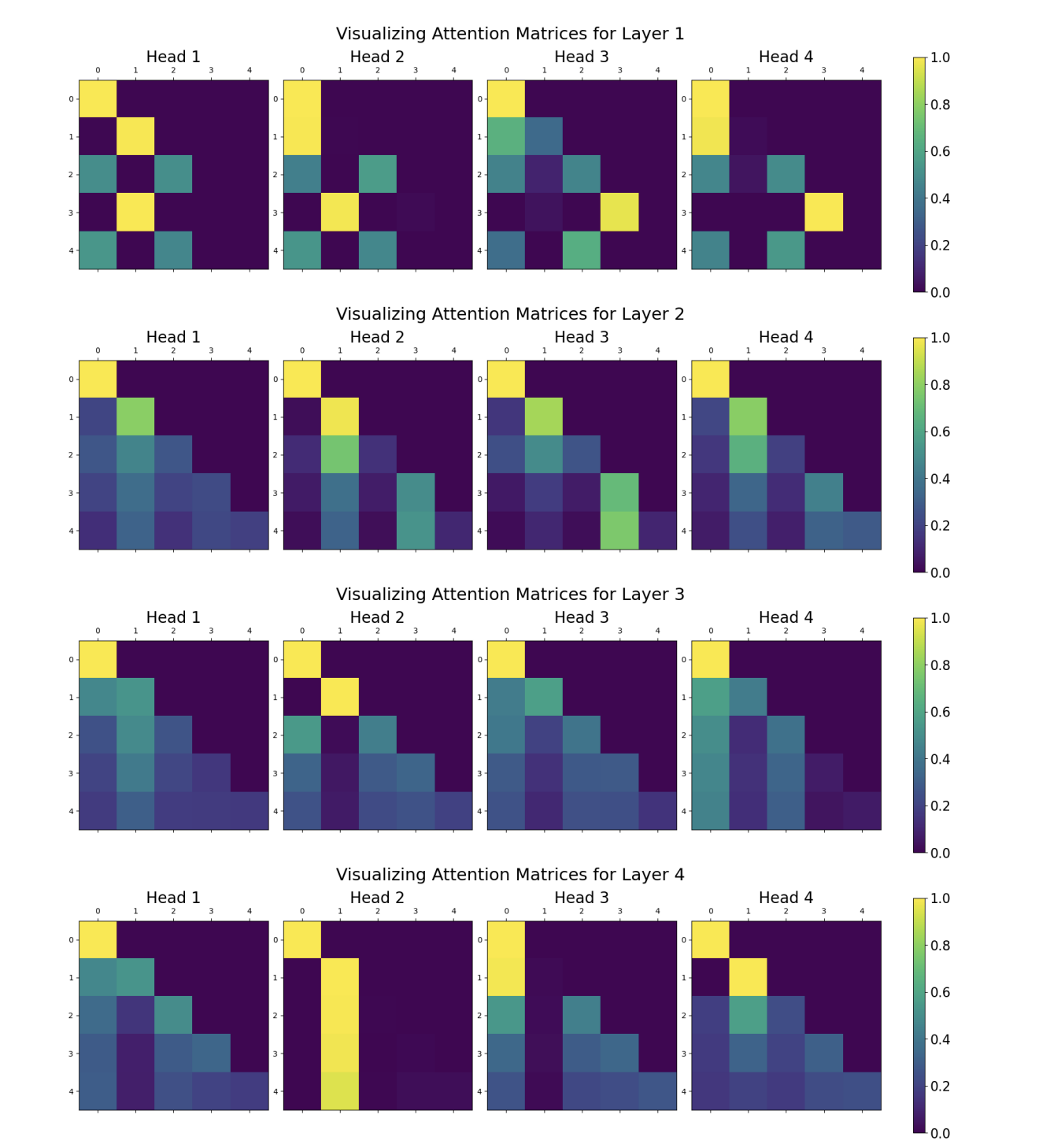
Observe that the attention matrices are lower-triangular matrices because of the mask that ensures that attention is only applied to the digits that appear to the left of the query digit (to maintain causality). Also observe that roughly, as we go deeper, the attention matrices remain somewhat similar but become less sparse (particularly from layer 1 to layer 2) as they start attending to more of the previous inputs. However, they consistently remain lower triangular matrices. Additionally, within a given layer, the attention matrices are sort of similar — for instance, between Head 3 and Head 4 for Layer 2